Hace unos días chateaba con un asesor de fondos de pensión, y noté que, por ignorancia o mala intención, el asesor decía que me era mejor poner plata en un fondo voluntario, a comisiones sobre saldo del 4%, que en el fondo obligatorio a comisiones sobre aportes de alrededor del 12%, porque, según la interpretación "4% es menos que 12% y para usted es mejor!".
No, ese 4% sobre saldos no es mejor que el 12% sobre depósito, pero no es fácil mostrarlo en un texto de chat.
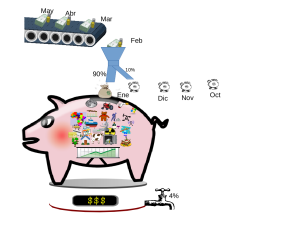
Entendamos que hay dos tipos principales de comisiones en Colombia(*):
- comisiones de entrada o pago o aporte -- un porcentaje del aporte mensual, lo que se llevan los hombrecitos de las bolsitas, en este ejemplo "10%".
- comisiones de administración -- un porcentaje del total del marrano, cada vez: lo que se va por el grifo de abajo (un grifo no era la mejor imagen -- o imagine que el grifo se abre una vez al año).
Como en clase de física donde al principio se estudian péndulos y planos sin fricción, consideremos el valor futuro de una inversión inicial $K_0$, que a lo largo de $n$ períodos de tiempo obtuvo rentabilidades $ r_1, r_2, ..., r_n$. Ese valor futuro será
$ VF = K_0 (1+r_1)(1+r_2)...(1+r_n) $
(Véase esta entrada para una explicación de las fórmulas.)
Efecto de comisión de entrada.
¿Cuál es el efecto de una comisión de entrada ($ C_E$) (cobrada sólo una vez, cuando el depósito se hace) en ese valor futuro?
$ VF_E = K_0 (1-C_E)(1+r_1)...(1+r_n)$
Al comparar $VF$ y $VF_E$,
$$ \frac{VF_E}{VF} = \frac{K_0 (1-C_E)(1+r_1)...(1+r_n)}{K_0 (1+r_1)(1+r_2)...(1+r_n)} = (1-C_E) $$
Por ejemplo, si la comisión de entrada fue 12%, ese será el efecto en el valor futuro (no importa cuán lejano o cercano): 12% menos.
(La "comisión de salida" es la cobrada cuando se saca la plata; es algebraicamente igual que la comisión de entrada. Por la ley de conmutación, $$K_0 (1-C_E)(1+r_1)...(1+r_n) = K_0(1+r_1)...(1+r_n)(1-C_E)$$: uno debería ser indiferente entre ellas si la tasa fuera la misma.
Efecto de comisión sobre saldo.
¿Cuál es el efecto de una comisión sobre saldo ($C_S$) (por la que, período a período, el saldo total hasta entonces acumulado se ve disminuido en esa proporción).
Suponiendo que la tasa de la comisióñ se mantiene estable a lo largo del tiempo,
$$VF_S = K_0(1+r_1)(1-C_S)(1+r_2)(1-C_S)...(1+r_n)(1-C_S)\\=K_0(1-C_S)^n(1+r_1)...(1+r_n)$$
(ver esta entrada si no se entiende la fórmula).
Al compararlas,
$$ \frac{VF_S}{VF} = \frac{K_0 (1-C_S)^n(1+r_1)...(1+r_n)}{K_0 (1+r_1)(1+r_2)...(1+r_n)} = (1-C_S)^n $$
El efecto de una comisión sobre saldo crece geométricamente con el número de periodos de inversión.
Es entonces evidente en la formulación que aunque $C_S$ sea mucho menor que $C_E$, (por ejemplo, $C_S=0.04=4\%$ como los cobrados por los administradores de fondos voluntarios de pensiones, frente a $C_E=0.115=11.5\%$ como lo que es típicamente cobrado en los fondos obligatorios), a lo largo del tiempo, cuando $(1-C_S)$ es compuesto periodo tras periodo, el efecto termina siendo mayor. Por ejemplo, si $C_E=33\%, (1-C_E)= 66\% $, pero
- $(1-0.04)^5 \approx 82\%$
- $(1-0.04)^{10} \approx 66\%$
- $(1-0.04)^{15} \approx 54\%$,
- $(1-0.04)^{20} \approx 44\%$,
- $(1-0.04)^{30} \approx 29\%$, etc.
Así que no se deje confundir, no caiga en esas situaciones donde escoger una opción con aparente ventaja lo lleva a la pérdida. Escoger una inversión con comisión sobre saldo del 4% (en vez de una que le quita un tercio de cada contribución) es sólo mejor hasta el décimo año; de ahí en adelante es muy mal negocio.
No hay comentarios.:
Publicar un comentario